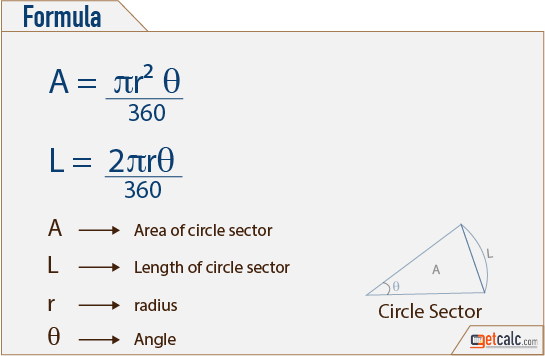
A simple closed shape where all points in a plane are at a given distance from a given point, the centre, is called a circle. The distance from the centre to the outside edge of the circle is called the radius. The formula by which the area of a circle is calculated is - Pir2, where Pi is the universal constant which is 3.14 and r is the radius. You can also calculate the area of the sector of a circle. The sector is an area that is enclosed by two radii and an arc. The area of the sector of a circle can be calculated by using the formula - (Q/360º) × Pir2, where Q is the angle subtended at the centre, measured in degrees.
To understand how to calculate square footage we must first begin with the definition of area. An area is the size of a two-dimensional surface. The area of a circle is the space contained within its circumference . To find out the area of a circle, we need to know its diameter which is the length of its widest part.
The diameter should be measured in feet for square footage calculations and if needed, converted to inches , yards , centimetres , millimetres and metres . Calculating areas and circumferences of circles plays an important role in almost all field of science and real life. For instance, formula for circumference and area of a circle can be applied into geometry. They are used to explore many other formulas and mathematical equations. An arch length is a portion of the circumference of a circle. The ratio of the length of an arc to the circumference is equal to the ratio of the measure of the arc to $360$ degrees.
A sector of a circles is the region bounded by two radii of the circle and their intercepted arc. For any other value for the length of the radius of a circle, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the area and lengths of parts of a circle. The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle. The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14.
Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle. In every day life ability to calculate area of rectangular shapes is more frequently required.
This perhaps is related to the fact that manufacturing process and transportation of most of the goods is easier if created with 90 degrees angles. All of those require simple multiplication of the dimensions of the area to achieve the required result. Circle calculations are performed less often in day to day life as significantly less circular objects can be found around us. However there are times when this calculation may be handy. Take for example quite popular inflatable pools for children.
The area of a circle calculation will be well handy to tell how much water is needed to fill the whole thing. To get the result it is enough to multiply the surface of the bottom with the depth of the pool. If you happen to be a princess with a liking for DIY you could use the equation when in need to replace the floor paneling in your round tower. Area of a circle is equal to the surface of a plane that is limited by a circle. In the matter of fact, geometry doesn't give width to borders of any of the shapes on the plane. Therefore in that sense the border of a circle doesn't have width and therefore it makes no sense to say whether the edge is included in the calculation or not.
Calculating area of a circle requires one simple computation where the radius has to be known. The remaining part of the equation is dependent on so called π value. This can be calculated to the required precision, if extreme accuracy is required.
Important thing to notice though is that exact calculation is not possible as it is impossible to find out the complete value of PI. In geometry, a circle is a set of all points in a plane that have the same distance to a point called the center of the circle. In other words, a circle is a locus of coplanar points equidistant from a certain point called the center.
The distance from any point of the circle to its center is called the radius. We used to view a circle as a round line or figure. However, a circle looks round only in Euclidean geometry. In some metric spaces, for example in the taxicab or Chebyshev's spaces the circles look rather square. Surface Area is the sum of all the areas that cover the surface of the object. The diameter is the distance across two extreme ends of a circle passing through the center.
The resultant value is the surface area of the circle. This concept can be of significance in geometry, to find the perimeter, area and volume of solids. Area of a circle calculator - calculating area of a circle online. Area of a circle - is a numerical characteristic that characterizes the size of a plane bounded by a circle line. Area of a circle can be calculated using the number pi and the radius of the circle, or using other known input data.
Our calculator will help you to calculate the area of a circle for free online or to check the already performed calculations. Since area is a measure of two dimensions, you always report area in square units like square inches or square feet . For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you. The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information.
The subject is always covered at some point at the Math or Geometry classes. Understanding the calculation is crucial for further advancement into more complex areas. Another explanation of the concept of the area of a circle is that it matches the number of square units that can be fitted inside the circle. This idea is easy to picture on a sheet of graph paper. Actually this set up can be used for alternative approximate calculation. Simply enter the desired value in the relevant box.
Please use only numbers (e.g. enter 22 not 22 cm). If you try to enter a unit of measure (e.g. 22 metres, 4 miles, 10 cm) you will get an NAN error appear in each box. When you have entered the number that you know, click the button on the right of that box to calculate all the other values. For example, if you know the volume of a sphere enter the value into the bottom box and then click the calculate button at bottom right. Here you can find calculation perimeter of circle, circumference or calculation area of circle and disc, length of disc formula. Diameter from circumference, formula of diameter, area of disc from circumference.
Formula for calculation of circle and for diameter, converter calculator. Roofing contractors can use a simple geometry and online calculators to figure out a roof area an... Reversing the same area of a circle equation we calculated that the radius of the circle in question is 2.24 m and the diameter being twice the length is 4.48 m.
The result has been rounded as it is not possible to exactly calculate the square root of number 5. A set of points in a plane equally distanced from a given point $O$ is a circle. The point $O$ is called the center of the circle. The distance from the center of a circle to any point on the circle is called the radius of this circle.A radius of a circle must be a positive real number. The circle with a center $O$ and a radius $r$ is denoted by $c$. In some real world situations, you may not be able to measure the diameter or radius accurately.
If the diameter is not drawn for you or the center is not identified, it can be difficult to approximate the center of a circle. A parallelogram is a quadrilateral that has two sets of parallel sides; a square, rectangle and a rhombus are all parallelograms. Unlike a square or a rectangle, the calculator calculates the area of a parallelogram by using the formula - base X height. The height of a parallelogram is the perpendicular distance between the two parallel sides or bases. An ellipse looks like a circle but is not a circle and is the group of all points on a plane whose distance from two fixed points sum up to a constant.
In an ellipse, you do not have a single radius but two different values. The values are taken from the centre to the two different edges of the ellipse called the semi-major and semi-minor axes. The calculator calculates the area by using the formula - Pi X a X b; here a and b are the distances of the two axes.
Area and circumference of circle calculator uses radius length of a circle, and calculates the perimeter and area of the circle. It is an online Geometry tool requires radius length of a circle. Using this calculator, we will understand methods of how to find the perimeter and area of a circle. Area of a circle calculator helps you to compute the area of a circle.
Using the area of a circle formula we can determine the region occupied by several objects such as wheels, rings, bangles, etc. To use the area of a circle calculator, enter the value of the radius in the given input box. A circle can be divided into many small sectors which can then be rearranged accordingly to form a parallelogram. When the circle is divided into even smaller sectors, it gradually becomes the shape of a rectangle.
We can clearly see that one of the sides of the rectangle will be the radius and the other will be half the length of the circumference, i.e, π. As we know that the area of a rectangle is its length multiplied by the breadth which is π multiplied to 'r'. A circle is a collection of points that are at a fixed distance from the center of the circle. We see circles in everyday life such as a wheel, pizzas, a circular ground, etc. The measure of the space or region enclosed inside the circle is known as the area of the circle. The most common error when using diameter is forgetting to square the denominator.
If you don't divide the diameter by 2 to find the radius, you can still find the area of the circle. However, you need to change the formula so that you square the 'd' otherwise your answer will be wrong. Circles show up all the time in the world around us so, naturally, being able to find the area of a circle is extremely useful in real life. For example, suppose you want to create a sandy beach area in your backyard in such a way that the beach is circular in shape. You need to figure out how much sand will be required and how much it's going to cost. The area A is equal to pi times the circumference divided by 2 times pi, squared.
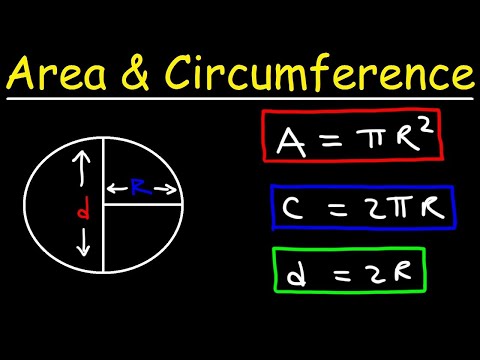
The area A is equal to pi times the diameter divided by 2, squared. Thus, the area of a circle A is equal to pi times the radius squared. The answer will be square units of the linear units, such as mm2, cm2, m2, square inches, square feet, and so on. Calculating area of a circle involves solving simple equation presented below.
The only necessary measurement needed is the radius, which is a distance from the center of a circle to its edge. The π number is usually approximated to two decimal places and therefore equals 3.14. Pi (π) is a non-algebraic number that represents the ratio of the distance around the circle to its diameter, usually estimated as 3.14. To solve for area, square the radius then multiply by 3.14. The first step for calculating the area of a circle from its diameter is to find that diameter. While math problems often list this value, in the real world, you must find the diameter yourself.
The diameter is the length of a line that begins at the edge of the circle, passes through the center of the circle, and ends at the opposite edge of the circle. To measure, you will need a ruler for small circles or a tape measure for large circles. The surface area and volume of a cylinder and cone with circular bases contain the formula for area of circle. The lateral surface of a cone consists of all segments that connect the vertex with points on the base. If we cut it along the slant height then the lateral surface is the sector of a circle. So, the lateral area of a cone also uses the formula for area of circle.
The diameter of the circle is double the radius of the circle. Hence the area of the circle formula using the diameter is equal to π/4 times the square of the diameter of the circle. The formula for the area of the circle, using the diameter of the circle π/4 × diameter2. The area of a circle formula is useful for measuring the region occupied by a circular field or a plot.
Suppose, if you have a circular table, then the area formula will help us to know how much cloth is needed to cover it completely. The area formula will also help us to know the boundary length i.e., the circumference of the circle. A circle is a two-dimensional shape, it does not have volume. A circle only has an area and perimeter/circumference. Let us learn in detail about the area of a circle, surface area, and its circumference with examples.
Use a protractor to measure the central angle made by the two radii. Set the base of the protractor along one of the radii, with the central point of the protractor aligned with the center of the circle. Then read the angle measurement that corresponds with the position of the second radius forming the sector. Our online calculators, converters, randomizers, and content are provided "as is", free of charge, and without any warranty or guarantee. Each tool is carefully developed and rigorously tested, and our content is well-sourced, but despite our best effort it is possible they contain errors.
We are not to be held responsible for any resulting damages from proper or improper use of the service. The area of the circle is the measure of the space or region enclosed inside the circle. In simple words, the area of a circle is the total number of square units inside that circle. If JavaScript is not working on your browser, or in case you are simply curious, here is the procedure for calculating the diameter of a circle from its area. For an example, we have an area of 303,000 square meters. A circle is a perfect shape because every part of the circle is the same distance from its center.
Like other perfect shapes, a circle is often used in architecture. Many famous buildings have circles as part of their architecture. Round buildings are hard to build; they require great technology and are expensive. Therefore, there has to be a strong motivation to build them.